常用的坐标系为地理坐标系(Geograpic Coordinate System,简称GCS)和投影坐标系(Projected Coordinate System,简称PCS)。
一、地理坐标系统
地理坐标系统(GCS)用一个三维的球面来确定地物在地球上的位置,地面点的地理坐标有经度、纬度、高程构成。地理坐标系统与选择的地球椭球体和大地基准面有关。椭球体定义了地球的形状,而大地基准面确定了椭球体的中心。
地理坐标系 (GCS) 使用三维球面来定义地球上的位置。GCS中的重要参数包括角度测量单位、本初子午线和基准面(基于旋转椭球体)。地理坐标系统中用经纬度来确定球面上的点位,经度和纬度是从地心到地球表面上某点的测量角。球面系统中的水平线是等纬度线或纬线,垂直线是等经度线或经线。这些线包络着地球,构成了一个称为经纬网的格网化网络。
GCS中经度和纬度值以十进制度为单位或以度、分和秒 (DMS) 为单位进行测量。纬度值相对于赤道进行测量,其范围是 -90°(南极点)到 +90°(北极点)。经度值相对于本初子午线进行测量。其范围是 -180°(向西行进时)到 180°(向东行进时)。
ArcGIS中,中国常用的坐标系统为GCS_Beijing_1954(Krasovsky_1940),GCS_Xian_1980(IAG_75),GCS_WGS_1984(WGS_1984),GCS_CN_2000(CN_2000)。
二、投影坐标系统
投影坐标系统是根据某种映射关系,将地理坐标系统中由经纬度确定的三维球面坐标投影到二维的平面上所使用的坐标系统。在该坐标系统中,点的位置是由(x,y,z)坐标来确定的。由于投影坐标是将球面展会在平面上,因此不可避免会产生变形。这些变形包括3种:长度变形、角度变形以及面积变形。通常情况下投影转换都是在保证某种特性不变的情况下牺牲其他属性。根据变形的性质可分为等角投影、等面积投影等。
我国的基本比例尺地形图(1:5千,1:1万,1:2.5万,1:10万,1:25万,1:50万,1:100万)中,大于或等于1:50万均采用高斯-克吕格投影(Gauss_Kruger),又叫横轴墨卡托投影(Transverse Mercator);1:100万的地形图采用正轴等角圆锥投影,又叫兰勃特投影(Lambert Conformal Conic);海上小于50万的地形图多用正轴等角圆柱投影,又叫墨卡托投影(Mercator)。在开发GIS系统中应该采用与我国基本比例尺地形图系列一致的地图投影系统。
下面是“1954北京坐标系” 投影坐标系统的空间参考描述:
Projection: Gauss_Kruger
False_Easting: 500000.000000 False_Northing: 0.000000 Central_Meridian: 99.000000 Scale_Factor: 1.000000 Latitude_Of_Origin: 0.000000 Linear Unit: Meter (1.000000)Geographic Coordinate System: GCS_Beijing_1954
Angular Unit: Degree (0.017453292519943299) Prime Meridian: Greenwich (0.000000000000000000) Datum: D_Beijing_1954 Spheroid: Krasovsky_1940 Semimajor Axis: 6378245.000000000000000000 Semiminor Axis: 6356863.018773047300000000 Inverse Flattening: 298.300000000000010000其中Projection: Gauss_Kruger这行描述了投影的类型,表示当前投影为高斯-克吕格投影。
False_Easting: 500000.000000表示坐标纵轴向西移动了500km,这样做是为了保证在该投影分带中所有x值都为正。 False_Northing: 0.000000表示横轴没有发生位移。 Central_Meridian: 99.000000表示中央经线位于经度为99度的位置。 Linear Unit: Meter (1.000000)表示在该投影下坐标单位为m。 Geographic Coordinate System: 以下描述了投影源的地理坐标系统参数。 可见每一个投影坐标系统都必会由一个地理坐标系统投影转化而成的。1.我国采用6度分带和3度分带:
1∶2.5万及1∶5万的地形图采用6度分带投影,即经差为6度,从零度子午线开始,自西向东每个经差6度为一投影带,全球共分60个带,用1,2,3,4,5,……表示.即东经0~6度为第一带,其中央经线的经度为东经3度,东经6~12度为第二带,其中央经线的经度为9度。
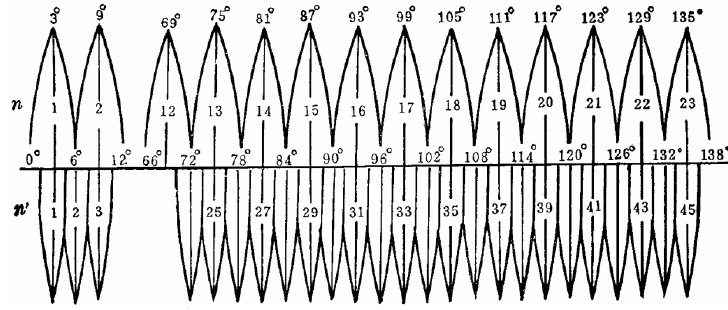
1∶1万的地形图采用3度分带,从东经1.5度的经线开始,每隔3度为一带,用1,2,3,……表示,全球共划分120个投影带,即东经1.5~ 4.5度为第1带,其中央经线的经度为东经3度,东经4.5~7.5度为第2带,其中央经线的经度为东经6度.我省位于东经113度-东经120度之间,跨第38、39、40共计3个带,其中东经115.5度以西为第38带,其中央经线为东经114度;东经115.5~118.5度为39带,其中央经线为东经117度;东经118.5度以东到山海关为40带,其中央经线为东经120度。
地形图上公里网横坐标前2位就是带号,例如:1∶5万地形图上的横坐标为20345486,其中20即为带号,345486为横坐标值。
2.当地中央经线经度的计算
六度带中央经线经度的计算:当地中央经线经度=6°×当地带号-3°,例如:地形图上的横坐标为20345,其所处的六度带的中央经线经度为:6°×20-3°=117°(适用于1∶2.5万和1∶5万地形图)。
三度带中央经线经度的计算:中央经线经度=3°×当地带号(适用于1∶1万地形图)。
3、如何计算当地的中央子午线?
当地中央子午线决定于当地的直角坐标系统,首先确定您的直角坐标系统是3度带还是6度带投影公式推算: 6度带中央子午线计算公式:当地经度/6=N;中央子午线L=6 * N (带号) 当没有除尽,N有余数时,中央子午线L=6*N - 3 3度带中央子午线计算公式: 当地经度/3=N;中央子午线L=3 X N 我国的经度范围西起 73°东至135°,可分成 六度带十一个(13号带—23号带),各带中央经线依次为(75°、81°、……123°、129°、135°);三度带二十二 个(24号带—45号带)。各带中央经线依次为(72°、75°、……132°、135°);
六度带可用于中小比例尺(如 1:250000)测图,三度带可用于大比例尺(如 1:10000)测图,城建坐标多采用三度带的高斯投影
4、如何判断投影坐标是3度带坐标还是6度带坐标
如(4231898,21655933)其中21即为带号,同样所定义的东伪偏移值也需要加上带号,如21带的东伪偏移值为21500000米。 假如你的工作区经度在120度至126度范围,则该坐标系为6度带坐标系,该带的中央经度为123度。 如(2949320,36353822)其中36即为带号,已知该地点位于贵阳市附近,而从地图上我们看到贵阳大概的经度是东经108度左右,因此可以36*3=108,所以该坐标系为3度带坐标系,该带的中央经度为108度。而不可能为6度带:36*6=216。三、基于ArcGIS的投影转换
在数据的操作中,我们经常需要将不同坐标系统的数据转换到统一坐标系下,方便对数据进行处理与分析,软件中坐标系转换常用以下两种方式:
3.1 直接采用已定义参数实现投影转换
ArcGIS软件中已经定义了坐标转换参数时,可直接调用坐标系转换工具,直接选择转换参数即可。工具位于ArcToolbox—Data management tools—Projections andtransfomations——Feature—Project(栅格数据投影转换工具 Raster—Project raster),在工具界面中输入以下参数:
Inputdataset:要投影的要素类、要素图层或要素数据集
OutputDataset:已在输出坐标系参数中指定坐标系的新要素数据集或要素类。
out_coor_system:已知要素类将转换到的新坐标系
GeographicTransformation:列表中为转换参数,以GCS_Beijing_1954转为GCS_WGS_1984为例,各转换参数含义如下:
Beijing_1954_To_WGS_1984_1 15918 鄂尔多斯盆地
Beijing_1954_To_WGS_1984_2 15919 黄海海域
Beijing_1954_To_WGS_1984_3 15920 南海海域-珠江口
Beijing_1954_To_WGS_1984_4 15921 塔里木盆地
Beijing_1954_To_WGS_1984_5 15935 北部湾
Beijing_1954_To_WGS_1984_6 15936鄂尔多斯盆地
3.2 自定义三参数或七参数转换
当ArcGIS软件中不能自动实现投影间直接转换时,需要自定义七参数或三参数实现投影转换,以七参数为例,转换方法如下:
3.2.1 自定义七参数地理转换
在ArcToolbox中选择Create CustomGeographic Transformation工具, 在弹出的窗口中,输入一个转换的名字,如wgs84ToBJ54。在定义地理转换方法下面,在Method中选择合适的转换方法如 COORDINATE_FRAME,然后输入七参数,即平移参数、旋转角度和比例因子。
3.2.2 投影转换
打开工具箱下的Projections and Transformations>Feature>Project,在弹出的窗口中输入要转换的数据以及Output Coordinate System,然后输入第一步自定义的地理坐标系如wgs84ToBJ54,开始投影变换
四、其他投影转换
1、proj4js
proj4js是一个转换点坐标从一个坐标系到另一个坐标系的JavaScript库,包括数据转换。这个库是由proj4和gctcp C库转换而来的JavaScript版本。
2、geotools
例子:最常用的两种坐标4326,3857,4326到3857转换
第一种方法
CoordinateReferenceSystem sourceCRS = CRS.decode("EPSG:4326");
CoordinateReferenceSystem targetCRS = CRS.decode("EPSG:3857");
MathTransform transform = CRS.findMathTransform(sourceCRS, targetCRS);
Coordinate coorDst=new Coordinate();
JTS.transform(new Coordinate(40, 116),coorDst, transform);
System.out.println(coorDst);
第二种方法
CoordinateReferenceSystem sourceCrs = CRS.decode("EPSG:4326");
CoordinateReferenceSystem targetCrs = CRS.decode("EPSG:3857");
boolean lenient = true;
MathTransform mathTransform = CRS.findMathTransform(sourceCrs, targetCrs, lenient);
DirectPosition2D srcDirectPosition2D = new DirectPosition2D(sourceCrs, 40, 116);//bj
DirectPosition2D destDirectPosition2D = new DirectPosition2D();
mathTransform.transform(srcDirectPosition2D, destDirectPosition2D);
double transX = destDirectPosition2D.x;
double transY = destDirectPosition2D.y;
System.out.println(transX);
System.out.println(transY);
https://blog.csdn.net/gisshixisheng/article/details/74370284